허민_동양수학은 없었나

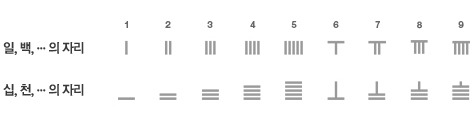
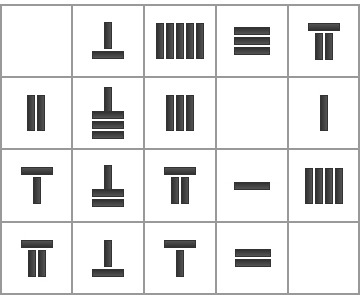
동양수학은 없었나?  

대학 수학 교과서는 물론이고, 초‧중등학교 수학 교과서에서도 동아시아 수학의 흔적을 찾아보기 어렵다. 수학을 위한 기호는 알파벳이고, 중요한 수학 결과는 모두 서양 수학자의 이름과 함께 등장한다. 도대체 우리의 조상은, 동아시아의 선조들은 수학에 기여한 바가 전혀 없는가? 동아시아의 수학 중에는 가르치고 배울 만한 내용은 없는가? 자연스럽게 이런 질문을 하게 되고, 자괴감에 빠지기도 한다.

 

 

수학의 역사를 다룬 대부분의 도서도 현재 수학의 패권을 차지하고 있는 서양 수학을 중심으로 이야기를 전개하고 있다. 사실, 수학의 역사를 기술하는 방법은 일반 역사를 기술하는 방법과 크게 다르지 않다. 고대 4대 문명 발상지의 수학을 기술하다가 그리스의 수학을 집중적으로 다룬다. 이후 유럽에게는 암흑시대인 중세를 거쳐 르네상스에 들어서면서부터는 완전히 유럽 중심으로 수학을 다룬다. 고대 4대 문명 발상지 중에서 인도와 중국의 고대 수학은 자료가 없어서 또는 자료에 접근하기 어려워서 연구하기 어렵다는 말과 함께 극히 단편적으로 취급할 뿐이다. 그러면서도 수학의 ‘보편성’을 내세워, 다른 문명 세계에 존재했던 수학은 잊어도 무방하다는 암시를 주고 있다.

 

 

분명히 동아시아에도 수학이 있었다. 동아시아의 전통 수학을 산학(算學 또는 筭學)이라 부른다. 이미 2000년 이전에 고전 구장산술(九章算術)을 통해 기틀을 다진 산학에는 당시의 사회에서 필요로 하는 것 이상이 담겨 있다. 이후 발전을 거듭해서 송‧원 시대에는 수학의 황금기에 이르렀다. 사실, 근세까지도 서양의 수학보다 동아시아의 산학이 여러 면에서 훨씬 앞서 있었다.

 

동아시아에서 피타고라스의 정리를 모를 리 없었고, 저명한 수학자 에릭 지만(Erik C. Zeeman, 1925～ ) 교수가 “피타고라스의 정리에 대한 세계에서 가장 아름다운 증명”이라고 극찬한 증명 방법도 고안했다. 유럽에서는 16, 17세기에서야 양수와 음수가 나타나고 그 연산 규칙은 그 후에서야 정립됐다. 그렇지만 동아시아에서는 양수와 음수 및 그 연산 규칙이 거의 기원전부터 정부술(正負術, 정은 양수, 부는 음수)이라는 이름으로 존재했었다. 연립 일차 방정식을 계수만으로 나타낸 다음에 정부술을 이용하고 소거법을 이용해서 이를 풀었다. 현재 중학교 2학년에서 배우는 소거법은 통상 가우스 소거법이라 하는데, 동아시아에서는 가우스(Johann Carl Friedrich Gauss, 1777～1855)가 태어나기 적어도 1500년 전부터 ‘가우스’ 소거법으로 연립 일차 방정식을 풀었다. 동아시아의 산학이 서양의 수학보다 앞섰던 내용은 더 들 수 있다. 이에 대한 소개는 다음 기회로 미루고, 이번에는 수학 용어와 일상 언어에 남아 있는 전통 산학의 흔적을 찾아보겠다.

 

 

 

동아시아에서는 계산 도구로 산대 또는 산가지를 아주 오래 전부터 사용했다. 수판으로 대체되기 전까지 산대는 중국에서는 명나라의 15세기 중반까지 그리고 우리나라에서는 19세기에도 계산 수단의 대종을 이루었다. 산대로 수를 나타내는 원리는 현재의 십진법과 같다. 오른쪽부터 왼쪽으로 나아가면서 일, 십, 백, 천, 만, ⋯의 자리를 정하고 각 자리에 산대를 늘어놓는데, 일, 백, 만…의 자릿수는 아래 그림의 첫 행과 같이 세우고, 십, 천…의 자릿수는 둘째 행과 같이 옆으로 뉘어서 표현했다. 그리고 6 이상은 편의를 위해 위쪽에 5를 나타내는 산대를 놓는다.

 

곱셈을 전통 수학에서는 승법(乘法)이라 했다. 한문에서 ‘A乘B’는 ‘A를 B에 곱한다’, 즉 ‘B×A’로서, ‘A’가 곱수(승수)이고 ‘B’가 곱하임수(피승수)이다. 여기서 ‘승(乘)’은 일상 언어에서 ‘타다’ 또는 ‘오르다’를 뜻한다. 승마(乘馬), 승차(乘車), 승선(乘船) 등을 생각하자. 그렇다면 곱셈은 왜 ‘올라타는 법’(乘法)일까?    예를 들면, 그림의 산판에 나타낸 수는 위로부터 차례로 6537, 28301, 67714, 76620을 나타낸다. 이렇게 나타낸 두 수를 더하거나 곱할 때는 그 두 수를 나타내는 산대를 위아래로 배치하고 자리를 옮기거나 해당하는 자릿수끼리 계산해서 답을 구했다. 그래서 다른 수보다 위에 ‘올라 타는’ 수가 생긴다. 동아시아에서는 전통적으로 곱셈을 덧셈의 축약 또는 거듭 더하기로 생각했었는데, 덧수(가수)들을 마부가 모는 말들로 생각했던 것으로 보인다.  그래서 곱셈이 올라타는 법, 승법이 된 것이다. 그러면 실제로 곱셈은 어떻게 산대로 계산 했을까?

 

실제로 전통적인 곱셈 과정을 보여주면 그림과 같다(편의를 위해 산대를 인도․아라비아 숫자로 나타냈다). 그 과정을 설명하면 다음과 같다. ①곱셈 78×46에서 곱수 46은 가장 위쪽에 위치하며 곱하임수 78 위에 ‘타고’ 있다. ②곱하임수 78을 한 자리씩 올린다. ③ 78과 곱수의 4(0)을 곱해서 312(0)을 얻는다. ④ 곱하임수 78을 한 자리씩 내린다. ⑤ 7(0)에 곱수의 6과 곱해서 얻은 42(0)를 더한다. ⑥ 8에 6을 곱한 48을 더한다, ⑦ 곱 3588을 얻는다. 곱하임수는 곱수 위에 올라타고 곱수를 이리저리 움직이면서 답을 얻는다.

 

 

 

 

 

곱셈 구구 또는 구구법은 중국에서 아주 오래 전부터 유래한 것으로 보이는데, 이와 관련된 이야기로 이미 춘추 시대(기원전 770～476)의 다음과 같은 것이 있다. 제(齊)나라의 환공(桓公)은 초현관(招賢館)을 만들어 뛰어난 인물을 등용하려고 했다. 오랫동안 기다렸지만, 아무도 응모하지 않았다. 1년 뒤 한 사람이 나타나서 환공에게 구구법을 말하면서 놀라운 지식이라고 뽐냈다. 환공은 이를 농담으로 생각하고 그에게 말했다. “당신은 구구법이 높은 지식이라고 생각하는가?” 그러자 그 사람이 대답했다. “사실, 구구법을 아는 것이 어떤 능력이나 학식이 있음을 보여주기에 충분하지 않습니다. 그러나 공께서 구구법만 아는 저를 등용하신다면, 틀림없이 유능하고 재주 많은 사람들이 관직에 나오려고 줄을 설 것입니다.” 환공이 이것이 온당한 주장이라고 생각해서, 그를 등용하고 환대했다. 그 뒤 한 달도 안 되어 곳곳으로부터 유능하고 재주 많은 사람들이 많이 응모했다. 한(漢)대의 곱셈 구구가 죽간에 표시되어 있는 것이 남아 있다. 여기에 나타난 곱셈 구구의 순서는 다음과 같다.

 

 

이렇게 고대의 곱셈 구구는 9×9=81에서 시작했다. 이에 따라 ‘곱셈 구구’ 또는 ‘구구법’이라는 이름이 붙었다. 이와 같이 처음 나타나는 대상을 그 주제의 이름으로 삼는 방법은 산학에서는 일반적이었다. 이를테면 동아시아 산학의 고전 구장산술에서 제1권은 여러 가지 밭의 넓이를 구하는 문제를 다루고 있는데, 그 이름은 <방전>이다. 바로 제1문에서 정사각형의 밭, 즉 방전(方田)의 넓이를 다루기 때문이다. 고대의 곱셈 구구는 9×9=81에서 시작해서 2×2=4에서 끝난다. 1～2세기까지도 이와 같았다. 곱셈 구구가 1×1=1까지 확장된 것은 5세기와 10세기 사이로, 4～5세기에 발간된 작자미상의 산학 책 ‘손자산경’(孫子算經)에 이와 같은 꼴이 있다. 송(宋)대의 13세기 또는 14세기에 이 순서가 역전되어 현재와 같이 1×1=1부터 시작해서 9×9=81로 끝나는 곱셈 구구로 바뀌었다.

 

 

분수는 작은 수를 나타내는 매우 유용한 수 표기 방법이고, 쓰임새도 많다. 산학에서는 분수 중에서도 자주 쓰이는 분수를 특별한 이름으로 불렀다. 이를테면 1/2은 중반(中半), 1/4은 약반(弱半), 3/4은 강반(强半)이라 했다. 그리고 1/3은 소반(少半), 2/3는 태반(太半)이라 했다. 약반, 강반, 소반은 생소하지만, 중반과 태반은 아주 익숙한 일상 언어이다. 수학을 전공하는 사람으로서, 이런 말이 산학의 수 이름이었다는 사실이 반갑기 그지없다.